2009年06月15日
中盤戦のイメージだけっす
ゲーム自体の説明、「詳しくはWebで!」方式にするっすかね?
ボードの説明部分にTouchすると飛ぶようにするってことっす。
テクスチャで可能かどうかを含めて、もう少し考えてみるっす。
どうもぺんぎんっす( ◎v◎ )
最終盤の攻防についてはこんな感じっす。
中盤での主導権の取り方については勉強中っす。
手詰まりになったときの鎖の本数について考えていけば、
必然と手が決まると思うんっすけどね。
イメージとしては、長くなりそうな鎖を「切って」、
本数を調整する感じっすかね?
テーマ図を用意できなかったんっすけど、
相手が切りたがっているのなら、それを防ぐ
っていうのも戦略っす。
長さを確定させてしまうってことっす。
モヤモヤとしたものはあるんっすけど、
図解できるほど固まってないっす。
勉強しないとっす・・・
ボードの説明部分にTouchすると飛ぶようにするってことっす。
テクスチャで可能かどうかを含めて、もう少し考えてみるっす。
どうもぺんぎんっす( ◎v◎ )
最終盤の攻防についてはこんな感じっす。
中盤での主導権の取り方については勉強中っす。
手詰まりになったときの鎖の本数について考えていけば、
必然と手が決まると思うんっすけどね。
イメージとしては、長くなりそうな鎖を「切って」、
本数を調整する感じっすかね?
テーマ図を用意できなかったんっすけど、
相手が切りたがっているのなら、それを防ぐ
っていうのも戦略っす。
長さを確定させてしまうってことっす。
モヤモヤとしたものはあるんっすけど、
図解できるほど固まってないっす。
勉強しないとっす・・・
2009年06月13日
実践編っす
ラインの色を微妙に変えたみたっす。
ボックスとの境界が分かりやすくなったっす。
裏面の説明も手を加えてみたっす。
あとは表面上部の隙間に入れるテクスチャっすね。
どうもぺんぎんっす( ◎v◎ )
前回記事の実践編っす。
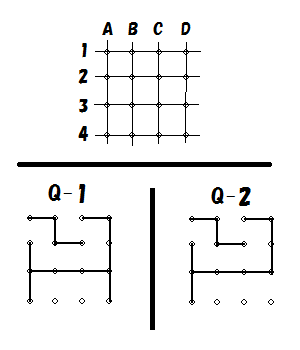
例題っす。画像を貼るのは初めてだったりするっす
ドットに名前を付けてあるっす。
で、ラインは[A1-A2]のように表わすことにするっす。
さて、Q-1は先手番、Q-2は後手番っす。
(ラインの本数を数えて、確認してみてくださいっす)
勝ちまでを読みきってくださいっす。
つまり、Q-1は先手が勝ち、Q-2は後手が勝つってことっすね。
Q-1とQ-2の違いは[D3-D4]があるかないかだけっす。
微妙な差が勝敗を分けてるっす。
さっそく解答と解説っす。
どちらの問題も上部の長さ6の鎖が勝敗を決めるっす。
つまり、下のボックスの獲得数は関係なく、
鎖を解かせたほうが勝ちっす。
上の鎖を解くと負けるのは分かってるっすから、
下の3つのボックスだけに注目して解説するっす。
A-1

正解は[B4-C4]に引くっす。
次に、後手が青で示されるラインのうちどちらかに引いたら
先手はもう片方の青で示したラインを取ればOKっす。
緑で示したものについても同様っす。
同じ色で示したラインについては見合いになってるっす。
すると後手はボックスを3つ獲得せざるをえず、
上の鎖も解いて、6-3で先手が勝つっす。
でも、これでも甘いっす。
例えば後手が[C3-C4](青のライン)に引いたとするっす。
すると、先手は[C4-D4]に引いてボックスを1つ獲得したのちに、
[A4-B4](青のライン)に引くという手が成立するっす。
6-3ではなく、結果は7-2っす。
取れるからといって、下全部を取ると負けるっすよ!
2つは相手にあげてくださいっす。
逆に[A4-B4]から後手が引いた場合も7-2で勝つんっすけど、
ちょっと違うっす。
[A4-B4]に引かれたら、先手は[B3-B4]に引いて
左下のボックスを取るっす。
次に引くのは[C4-D4]っす。
後手は[C3-C4]の1択っすから、キマるっす。
左右同型っすから、緑も同じようにすれば7-2で勝てるっす。
**ポイント**
どのパターンでも先手が長さ2の鎖を作っているっす。
これは「ドミノを作る」という手筋っす。
相手に手番を渡すときに頻繁に出てくる形っす。
ボックスを取ることが必ずしも勝敗に影響するのではない、
っていうことっすね。
Q-2はオマケっす。
もう後手は負けようがないんっすけど、しっかりと
読み切ってくださいっす。
解答の1例を「続きを読む」に載せておくっす。
続きを読む
ボックスとの境界が分かりやすくなったっす。
裏面の説明も手を加えてみたっす。
あとは表面上部の隙間に入れるテクスチャっすね。
どうもぺんぎんっす( ◎v◎ )
前回記事の実践編っす。

例題っす。画像を貼るのは初めてだったりするっす
ドットに名前を付けてあるっす。
で、ラインは[A1-A2]のように表わすことにするっす。
さて、Q-1は先手番、Q-2は後手番っす。
(ラインの本数を数えて、確認してみてくださいっす)
勝ちまでを読みきってくださいっす。
つまり、Q-1は先手が勝ち、Q-2は後手が勝つってことっすね。
Q-1とQ-2の違いは[D3-D4]があるかないかだけっす。
微妙な差が勝敗を分けてるっす。
さっそく解答と解説っす。
どちらの問題も上部の長さ6の鎖が勝敗を決めるっす。
つまり、下のボックスの獲得数は関係なく、
鎖を解かせたほうが勝ちっす。
上の鎖を解くと負けるのは分かってるっすから、
下の3つのボックスだけに注目して解説するっす。
A-1

正解は[B4-C4]に引くっす。
次に、後手が青で示されるラインのうちどちらかに引いたら
先手はもう片方の青で示したラインを取ればOKっす。
緑で示したものについても同様っす。
同じ色で示したラインについては見合いになってるっす。
すると後手はボックスを3つ獲得せざるをえず、
上の鎖も解いて、6-3で先手が勝つっす。
でも、これでも甘いっす。
例えば後手が[C3-C4](青のライン)に引いたとするっす。
すると、先手は[C4-D4]に引いてボックスを1つ獲得したのちに、
[A4-B4](青のライン)に引くという手が成立するっす。
6-3ではなく、結果は7-2っす。
取れるからといって、下全部を取ると負けるっすよ!
2つは相手にあげてくださいっす。
逆に[A4-B4]から後手が引いた場合も7-2で勝つんっすけど、
ちょっと違うっす。
[A4-B4]に引かれたら、先手は[B3-B4]に引いて
左下のボックスを取るっす。
次に引くのは[C4-D4]っす。
後手は[C3-C4]の1択っすから、キマるっす。
左右同型っすから、緑も同じようにすれば7-2で勝てるっす。
**ポイント**
どのパターンでも先手が長さ2の鎖を作っているっす。
これは「ドミノを作る」という手筋っす。
相手に手番を渡すときに頻繁に出てくる形っす。
ボックスを取ることが必ずしも勝敗に影響するのではない、
っていうことっすね。
Q-2はオマケっす。
もう後手は負けようがないんっすけど、しっかりと
読み切ってくださいっす。
解答の1例を「続きを読む」に載せておくっす。
続きを読む
2009年06月12日
最終盤の解説っす
「Dots and Boxes」「Boxes game」で検索すると、
いろいろ見つかると思うっす。
英語っすけど・・・
そんなわけで、自分なりに攻略法を書いてみようと思うっす。
盤のサイズはボックスで3×3で固定っす。
飽きたら終了っす!
どうもぺんぎんっす( ◎v◎ )
第1回目ということなので、テーマは「最終盤」っす。
間違わなければ勝敗はすでに決している状態っす。
この「間違わなければ」がクセモノっす。
最終盤では
「どこに引いても相手にボックスを取られてしまう」状態になるっす。
手詰まりっすね。
このとき、いくつかの鎖(chain)に分かれていると思うっす。
鎖の中で、どれか1本を引くとバタバタと連続して取れるっすね。
ここで例を示せると良いんっすけど・・・
以下は鎖に分断された状態での攻防についてっす。
数学的にややこしい話をカットして、
・鎖の「本数」が偶数なら先手の勝ち
・鎖の「本数」が奇数なら後手の勝ち
これを覚えてくださいっす。
ただし、獲得済みボックスがあると入れ替わったりするっす。
ここら辺は説明が面倒なので、ボックスは全て空き状態ということで
話を進めるっす。
これは中盤の戦術のときにでも書くっす。
解説と勝ちまでの手順っす。
パターン1. 鎖の「本数」が2本
ボックスの総数は9個っす。
で、鎖の本数は2本っす。
ということは、鎖の長いほうと短いほうが存在するっす。
これは以下も共通なんっすけど、
手詰まり状態になったとき、鎖を解くことになるのは必ず先手番
ってことっす。
鎖を「解く」というのは、残りの2つのラインのうち片方にラインを引く、
っていう意味っす。
用語の解説しながらはキツイっす・・・
手詰まり状態のとき、各鎖は2つのラインを残して全て塞がってるっす。
つまり、残りのラインの数は2 × (鎖の本数)になってるっす。
これは偶数になるっすね。
で、ラインの総数は24本っす。
どのボックスも取られていないとき、交互にラインを引いていくっすから、
「手詰まり状態になったとき、鎖を解くことになるのは必ず先手番」
っていうのは確認できると思うっす。
話を戻すっす。
「手詰まり状態になったとき、鎖を解くことになるのは必ず先手番」
ということは、もう分かった方もいると思うんっすけど、
鎖の「本数」が2本の状態は先手の勝ちっす。
解く鎖は2本のうちの短いほうっす。
相手に短い鎖は取られるっすけど、
相手は必ず長い鎖を解かなければばらなくなるっす。
結果、先手の逆転勝ち・・・というふうに見えるんっすけど、
もっと前に勝ちは見えてるわけっす。
先手番の気持ち良い勝ち方っすね。
パターン2. 鎖の「本数」が3本
ついてきてるっすか?
さらにややこしくなるっすよ?
結論は先に書いた通り、後手の勝ちっす。
鎖の「長さ」について、X ≦ Y ≦ Z が成り立っているとするっす。
ここで手番は先手番っす。
先手番のプレイヤーは一番短い長さXの鎖を解いて手番を渡すっす。
すると後手番のプレイヤーは長さXの鎖を獲得したのち、
次に短い長さYの鎖を解くっす。
先手番のプレイヤーは長さYの鎖を取って、残った長さZの鎖を解くっす。
最後に長さZの鎖を後手番のプレイヤーが取ってゲームセットっす。
結果は
先手: Y
後手: X + Z
で、後手番の勝ちっす。
では、先手番のプレイヤーが最初に長さXの鎖を解かなかった場合っす。
つまり長さYまたは長さZの鎖を解いた場合っす。
これはもっとヒドイ結果になるっす。
先: 長さYまたは長さZの鎖を解く。
後: 解かれた鎖を獲得。今度は長さXの鎖を解く。
先: 長さXの鎖を獲得。残った長さYまたは長さZの鎖を解く
後: 残りを獲得
結果は
先: X
後: Y + Z
となって、スコアが悪くなっちゃうっす。
まあ、どちらにせよ間違わなければ後手の勝ちっす。
以下4本、5本の場合も同じように考察していくと
最初のほうに書いた
・鎖の「本数」が偶数なら先手の勝ち
・鎖の「本数」が奇数なら後手の勝ち
っていうのが確認できると思うっす。
以上のことを知っているだけで、少しは勝率上がるんじゃないっすかね?
いろいろ見つかると思うっす。
英語っすけど・・・
そんなわけで、自分なりに攻略法を書いてみようと思うっす。
盤のサイズはボックスで3×3で固定っす。
飽きたら終了っす!
どうもぺんぎんっす( ◎v◎ )
第1回目ということなので、テーマは「最終盤」っす。
間違わなければ勝敗はすでに決している状態っす。
この「間違わなければ」がクセモノっす。
最終盤では
「どこに引いても相手にボックスを取られてしまう」状態になるっす。
手詰まりっすね。
このとき、いくつかの鎖(chain)に分かれていると思うっす。
鎖の中で、どれか1本を引くとバタバタと連続して取れるっすね。
ここで例を示せると良いんっすけど・・・
以下は鎖に分断された状態での攻防についてっす。
数学的にややこしい話をカットして、
・鎖の「本数」が偶数なら先手の勝ち
・鎖の「本数」が奇数なら後手の勝ち
これを覚えてくださいっす。
ただし、獲得済みボックスがあると入れ替わったりするっす。
ここら辺は説明が面倒なので、ボックスは全て空き状態ということで
話を進めるっす。
これは中盤の戦術のときにでも書くっす。
解説と勝ちまでの手順っす。
パターン1. 鎖の「本数」が2本
ボックスの総数は9個っす。
で、鎖の本数は2本っす。
ということは、鎖の長いほうと短いほうが存在するっす。
これは以下も共通なんっすけど、
手詰まり状態になったとき、鎖を解くことになるのは必ず先手番
ってことっす。
鎖を「解く」というのは、残りの2つのラインのうち片方にラインを引く、
っていう意味っす。
用語の解説しながらはキツイっす・・・
手詰まり状態のとき、各鎖は2つのラインを残して全て塞がってるっす。
つまり、残りのラインの数は2 × (鎖の本数)になってるっす。
これは偶数になるっすね。
で、ラインの総数は24本っす。
どのボックスも取られていないとき、交互にラインを引いていくっすから、
「手詰まり状態になったとき、鎖を解くことになるのは必ず先手番」
っていうのは確認できると思うっす。
話を戻すっす。
「手詰まり状態になったとき、鎖を解くことになるのは必ず先手番」
ということは、もう分かった方もいると思うんっすけど、
鎖の「本数」が2本の状態は先手の勝ちっす。
解く鎖は2本のうちの短いほうっす。
相手に短い鎖は取られるっすけど、
相手は必ず長い鎖を解かなければばらなくなるっす。
結果、先手の逆転勝ち・・・というふうに見えるんっすけど、
もっと前に勝ちは見えてるわけっす。
先手番の気持ち良い勝ち方っすね。
パターン2. 鎖の「本数」が3本
ついてきてるっすか?
さらにややこしくなるっすよ?
結論は先に書いた通り、後手の勝ちっす。
鎖の「長さ」について、X ≦ Y ≦ Z が成り立っているとするっす。
ここで手番は先手番っす。
先手番のプレイヤーは一番短い長さXの鎖を解いて手番を渡すっす。
すると後手番のプレイヤーは長さXの鎖を獲得したのち、
次に短い長さYの鎖を解くっす。
先手番のプレイヤーは長さYの鎖を取って、残った長さZの鎖を解くっす。
最後に長さZの鎖を後手番のプレイヤーが取ってゲームセットっす。
結果は
先手: Y
後手: X + Z
で、後手番の勝ちっす。
では、先手番のプレイヤーが最初に長さXの鎖を解かなかった場合っす。
つまり長さYまたは長さZの鎖を解いた場合っす。
これはもっとヒドイ結果になるっす。
先: 長さYまたは長さZの鎖を解く。
後: 解かれた鎖を獲得。今度は長さXの鎖を解く。
先: 長さXの鎖を獲得。残った長さYまたは長さZの鎖を解く
後: 残りを獲得
結果は
先: X
後: Y + Z
となって、スコアが悪くなっちゃうっす。
まあ、どちらにせよ間違わなければ後手の勝ちっす。
以下4本、5本の場合も同じように考察していくと
最初のほうに書いた
・鎖の「本数」が偶数なら先手の勝ち
・鎖の「本数」が奇数なら後手の勝ち
っていうのが確認できると思うっす。
以上のことを知っているだけで、少しは勝率上がるんじゃないっすかね?


